A Série de Fourier é uma ferramenta de extrema importância para diversas áreas de conhecimento, especialmente para as engenharias, tendo aplicação direta nas áreas da engenharia elétrica, acústica, óptica, processamento de sinais e processamento de imagens, por exemplo. O enunciado clássico da Série de Fourier é:

"Toda função periódica pode ser representada pela pela soma de senos e cossenos, os quais são harmônicamente relacionados."

A série de Fourier pode ser expressa de diversas formas; existe a forma exponencial (que será utilizada nesse post), a forma trigonométrica e a forma compacta. Independente da forma que você opte por utilizar, o resultado será o mesmo garantido pelo enunciado acima. O nosso esforço, em todos os casos, será apenas obter os coeficientes da série. Diante disso, o objetivo desse post é apresentar os cálculos necessários para a obtenção dos coeficientes da série expoencial de um sinal quadrado e, em seguida, a impementação de um algoritmo em Python para a visualização do sinal resultante dos cálculos realizados.

Cálculo da Série de Fourier Exponencial

Para os nossos cálculos, utilizaremos a função quadrada que é representada pela figura abaixo:

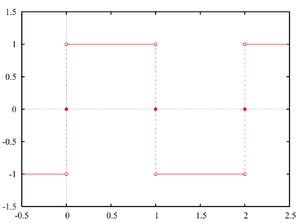
Implementação da Série de Fourier em Python

Tendo em vista que temos os coeficientes da série de Fourier exponencial complexa do sinal quadrado, podemos escrever o código que execute essa função x(t), o qual é apresentado abaixo:

import matplotlib.pyplot as plt
import numpy as np
from math import pi

t = np.arange(-4, 4, 0.001)

def square_serie(Nh):
    x = np.zeros(t.shape).astype('complex128')

    for k in range(1, (2 * Nh) + 1, 2):
        x += (2 / (1j * k * pi)) * np.exp(1j * k * pi * t)
    
    return x

plt.figure(figsize=(12,8))
plt.subplot(221)
plt.title('3 harmônicos')
plt.plot(t, np.real(square_serie(3)))
plt.subplot(222)
plt.title('10 harmônicos')
plt.plot(t, np.real(square_serie(10)))
plt.subplot(223)
plt.title('50 harmônicos')
plt.plot(t, np.real(square_serie(50)))
plt.subplot(224)
plt.title('1000 harmônicos')
plt.plot(t, np.real(square_serie(1000)))
plt.tight_layout()

Observe que, após a importação das bibliotecas necessárias para a implementação do código, foi criado um numpy array que representa o tempo; nesse caso, estaremos plotando o nosso sinal no intervalo entre -4 e 4, com amostras espaçadas uniformemente, com um passo de 0,001. Em seguida, foi criada uma função (square_serie), que calcula a série de fourier da onda quadrada, recebendo como parâmetro o número de harmônicos desejados (Nh), que corresponde ao limite superior do somatório.

Dentro da função é criado um array x, iniciando com zero, tendo o mesmo tamanho do array do tempo (t), o qual irá conter os valores da amplitude do sinal, ou seja, o resultado do somatório da série. Esse somatório, por sua vez, é definido pelo for, que inicia em 1, encerra em 2×Nh (lembre-se que o +1 é necessário, visto que queremos incluir o 2×Nh; caso contrário, o for encerraria antes disso), e tem um passo 2, uma vez que ak=0 quando k é par.

A função square_serie retorna o resultado do somatório da série e, dessa forma, foi utilizado a biblioteca do matplotlib para plotar os gráficos da série de Fourier dessa onda quadrada, considerando diferentes números de harmônicos (3, 10, 50 e 1000). O resultado é apresentado na figura abaixo.

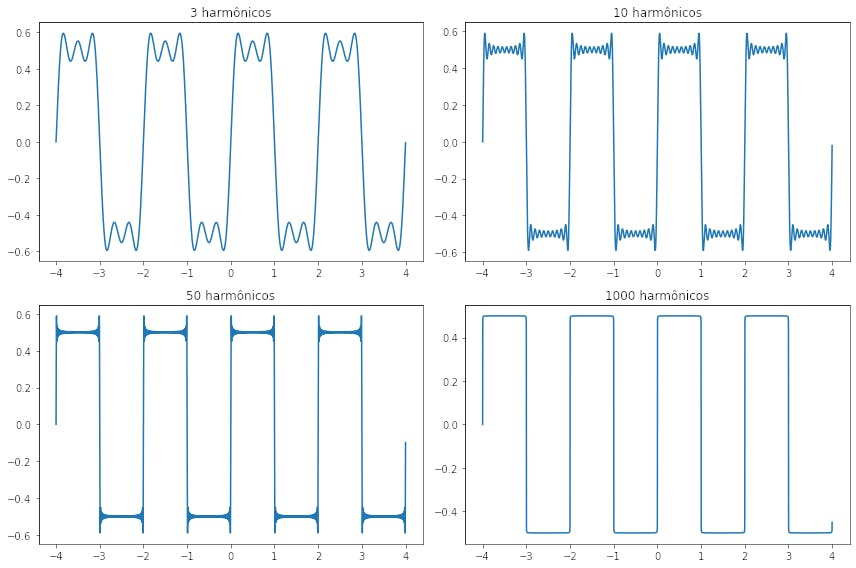
Note que, à medida que o número de harmônicos tende ao infinito, o sinal resultante da série se aproxima do sinal original, comprovando assim o enunciado da série de Fourier. Com 1000 harmônicos o sinal já é bem semelhante àquele apresentado na primeira imagem desse post, não é mesmo?

Gostou desse post? Então, não deixa de me seguir no Instagram ou no Canal do Telegram para acompanhar todas as novidades do Blog e do canal do YouTube. Um abraço e até a próxima!